Understanding the Fundamental Operation of Addition in Mathematics
At the core of arithmetic and broader mathematical sciences lies the operation of addition, a process that captures the essence of combining quantities into unified totals. Not only does addition serve as one of the earliest learned mathematical concepts, but it also forms the backbone of more advanced theories, computations, and practices across multiple disciplines. Its ubiquity in daily life—from balancing a checkbook to calculating distances—highlights its vital importance. This article, curated for the Free Source Library platform (freesourcelibrary.com), aims to delve into every aspect of addition, examining its definitions, properties, variations across different number systems, and its extensive practical applications.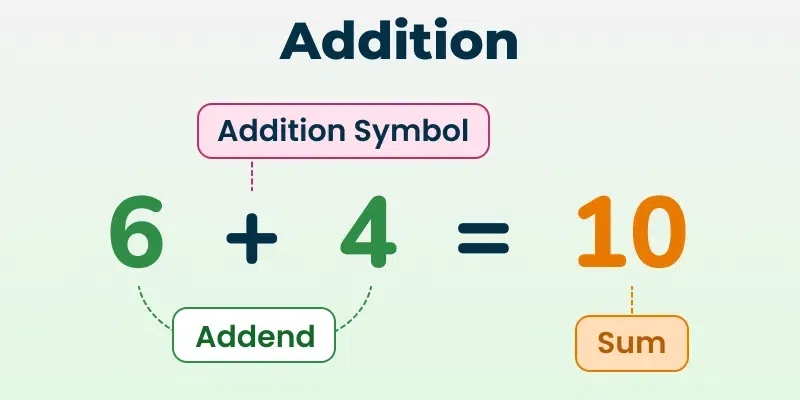
Defining Addition: The Fundamental Concept
The Core Idea of Adding Quantities
In essence, addition is a process whereby two or more quantities are combined to produce a single new quantity. It is a binary operation, which involves precisely two operands—these are the quantities being summed. The operation results in a single output known as the sum. For instance, consider adding the numbers 3 and 5:
Example of Basic Addition
3 + 5 = 8
- Operands (Addends): 3 and 5
- Result (Sum): 8
This simple operation embodies the fundamental principle of aggregation—combining smaller parts into a larger whole. The plus sign (+), universally recognized symbol, signifies this action across all levels of mathematics. Addition extends beyond just numbers; it also applies to objects, counts, and abstract quantities in diverse mathematical contexts.
Properties of Addition: Underlying Mathematical Principles
The utility and universality of addition are largely attributed to its intrinsic properties, which facilitate flexible manipulation and calculation. These properties include:
Commutativity
The commutative property states that the order of the addends does not influence the sum. Mathematically:
a + b = b + a
This property simplifies problem-solving by allowing the rearrangement of terms for easier calculation. For example:
Example:
4 + 6 = 6 + 4 = 10
Associativity
The associative property emphasizes that when adding three or more numbers, how the operands are grouped does not change the sum:
(a + b) + c = a + (b + c)
This is crucial when dealing with lengthy sums, as it permits regrouping without changing the outcome. For example:
Example:
(2 + 3) + 4 = 2 + (3 + 4) = 9
Identity Element
The additive identity is the number zero. Adding zero leaves any number unchanged:
a + 0 = a
For instance:
7 + 0 = 7
Inverse Property
Every number has an additive inverse, which is its negative. When a number and its inverse are added, the result is zero:
a + (-a) = 0
Examples include:
5 + (-5) = 0
These properties are foundational in simplifying expressions, solving equations, and understanding the structure of numbers and operations.
Expansion of Addition in Different Number Systems
Natural Numbers
The simplest set where addition is defined is the set of natural numbers (\(\mathbb{N}\)), beginning at 1 and extending infinitely: 1, 2, 3, 4, … These numbers adhere strictly to the properties already discussed, with no exceptions.
Whole Numbers
Extending the natural numbers, the set of whole numbers (\(\mathbb{W}\)) includes zero. Addition involving zero in this set preserves the identity property:
a + 0 = a
Integers
The set of integers (\(\mathbb{Z}\)) encompasses positive numbers, negative numbers, and zero. Addition here involves carefully handling the effects of combining positive and negative integers, which can result in positive, negative, or zero as output. For example:
| Expression | Result | Explanation |
|---|---|---|
| 3 + (-5) | -2 | The magnitude of -5 is larger, so the sum is negative. |
| -4 + 7 | 3 | A positive sum as the positive number exceeds the negative. |
Rational Numbers
Rational numbers (\(\mathbb{Q}\)) include fractions where numerator and denominator are integers, with the denominator non-zero. Addition often necessitates creating a common denominator before summing fractions:
Example:
\(\frac{1}{3} + \frac{2}{3} = \frac{3}{3} = 1\)
Real Numbers
The set of real numbers (\(\mathbb{R}\)) combines rational and irrational numbers. Addition in this set can involve more complex quantities, like irrational roots:
Example:
\(\sqrt{2} + \sqrt{3}\) cannot be simplified into a rational number but remains a real number.
Complex Numbers
Complex numbers are expressed as \(a + bi\) with real parts and imaginary parts. Addition involves combining real parts and imaginary parts separately:
(a + bi) + (c + di) = (a + c) + (b + d)i
Example:
(3 + 2i) + (4 + 5i) = 7 + 7i
Advanced Mathematical Fields and the Role of Addition
Algebra
In algebra, addition facilitates the simplification of expressions and the isolation of variables. For instance, solving an equation like \(x + 5 = 12\) requires subtracting 5 from both sides, which is inverse to addition. The ability to manipulate algebraic structures relies heavily on the properties of addition.
Differential and Integral Calculus
Calculus depends fundamentally on the ideas of summing infinitesimal quantities—integrals—where the addition of infinitely small parts yields areas and volumes. Derivatives are defined by limits involving sums and differences, illustrating the importance of addition at a conceptual level.
Set Theory and Union Operations
While the union of sets is not precisely addition, it shares algebraic properties such as commutativity and associativity, illustrating how the concept of combining elements extends beyond numbers.
Linear Algebra and Vector Addition
Vectors—arrows describing quantities with magnitude and direction—are added component-wise in linear algebra. This operation is central to solving systems of equations, geometric transformations, and high-dimensional space analysis:
Vector Addition Example:
\(\vec{u} = (1, 2, 3)\), \(\vec{v} = (4, 5, 6)\)
\(\vec{u} + \vec{v} = (1+4, 2+5, 3+6) = (5, 7, 9)\)
Real-World Applications of Addition
- Financial Calculations: Summing expenses, incomes, balances, and profits to determine overall financial status.
- Measurement and Engineering: Adding lengths, weights, volumes, and forces in practical situations like construction or mechanical design.
- Statistics and Data Analysis: Summing data points, calculating averages, and determining totals in research and surveys.
- Computer Science: Binary addition, algorithm execution, data structures, and memory address calculations frequently rely on addition.
- Physics: Combining forces, summing velocities, and adding energies are all underpinned by addition principles.
Historical and Philosophical Perspectives on Addition
The development of addition as a mathematical operation dates back thousands of years. Ancient civilizations such as the Babylonians, Egyptians, and Greeks contributed to understanding and formalizing the concept. The earliest systems of tallying, counting, and recording were simple yet depicted the fundamental need of aggregating quantities.
Philosophically, addition embodies the human inclination towards categorization and combination for better understanding and manipulation of the environment. It reflects a natural cognitive process that extends from basic counting to highly abstract theories, demonstrating its central role in our quest for knowledge.
Mathematical Challenges and Open Problems Related to Addition
Despite its apparent simplicity, addition has played a part in complex mathematical conjectures and problems. For example, the famous Goldbach Conjecture—proposing that every even number greater than 2 can be expressed as the sum of two primes—remains unresolved, illustrating ongoing questions rooted in additive processes.
Similarly, problems involving partitions, sums of special number sequences, and additive bases continue to inspire research, pushing the boundaries of number theory and combinatorics.
Summary Data: Properties of Addition in Different Number Sets
| Number System | Closure Under Addition | Commutativity | Associativity | Identity Element | Remarks |
|---|---|---|---|---|---|
| Natural Numbers (\(\mathbb{N}\)) | Yes | Yes | Yes | None | Addition of natural numbers results in natural numbers, but zero is often excluded. |
| Whole Numbers (\(\mathbb{W}\)) | Yes | Yes | Yes | 0 | Zero included; addition with zero preserves numbers. |
| Integers (\(\mathbb{Z}\)) | Yes | Yes | Yes | 0 | Includes negatives; addition remains closed. |
| Rational Numbers (\(\mathbb{Q}\)) | Yes | Yes | Yes | 0 | Requires common denominators for fractions before addition. |
| Real Numbers (\(\mathbb{R}\)) | Yes | Yes | Yes | 0 | Includes irrationals, extending the real number line infinitely. |
| Complex Numbers (\(a+bi\)) | Yes | Yes | Yes | 0 + 0i | Component-wise addition of real and imaginary parts. |
Conclusion: The Essential Role of Addition
Recognizing addition as more than just a basic arithmetic operation underscores its vast significance across the scientific, mathematical, and everyday spectrum. From elementary counting to the deepest theories of abstract algebra and calculus, addition remains central, unifying various mathematical domains through its fundamental properties. Its adaptability across diverse systems—natural, integer, rational, real, and complex—demonstrates its enduring importance in decoding the universe’s numerical fabric.
As mathematics continues to evolve, addition will undoubtedly remain a cornerstone operation, facilitating advancements in theoretical research and practical applications alike. Its simplicity belies a depth that continues to inspire curiosity, challenge mathematicians, and underpin the complex structures of modern science and technology.
For further exploration and comprehensive resources, visit the Free Source Library platform (freesourcelibrary.com), which provides invaluable access to knowledge on foundational and advanced mathematical concepts.



